Machine Learning Techniques - 2

ML techniques and Good practices

Table of Contents

A: All models are wrong

In-sample and Out-sample

In-sample error: Calculated from data used for training.

Out-sample error: Calculated from unseen data (not used in training)

2 sampling with n = 10

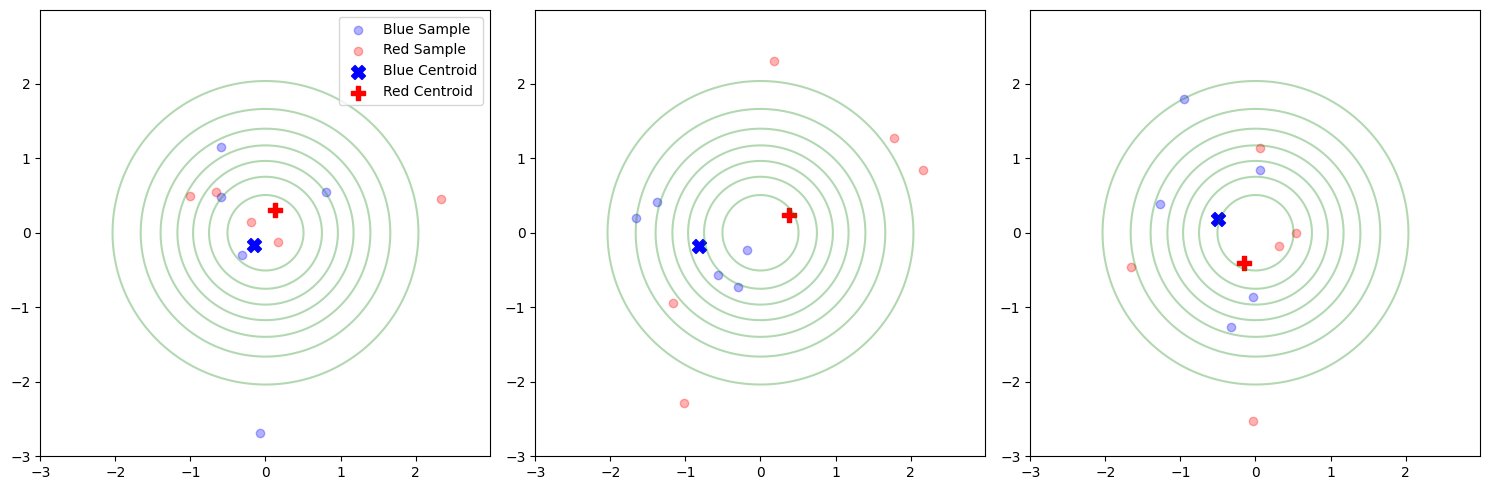
In-sample and Out-sample

Importance of validating using unseen data.

2 sampling with n = 50

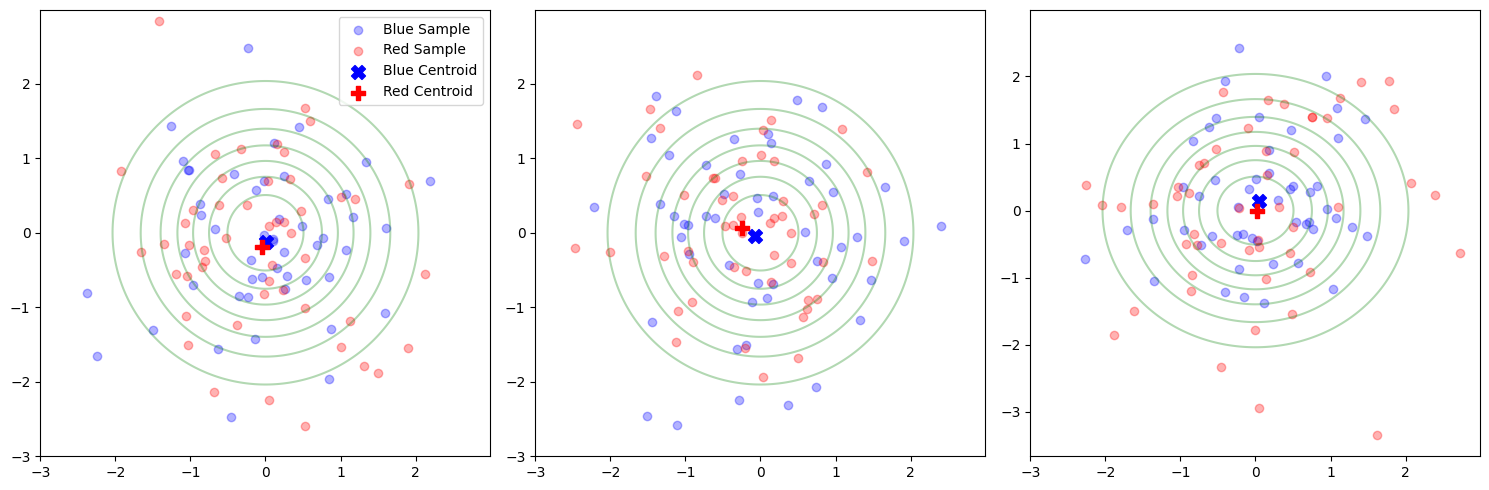
In-sample and Out-sample

Difference are lower with larger samples.

2 sampling with n = 500

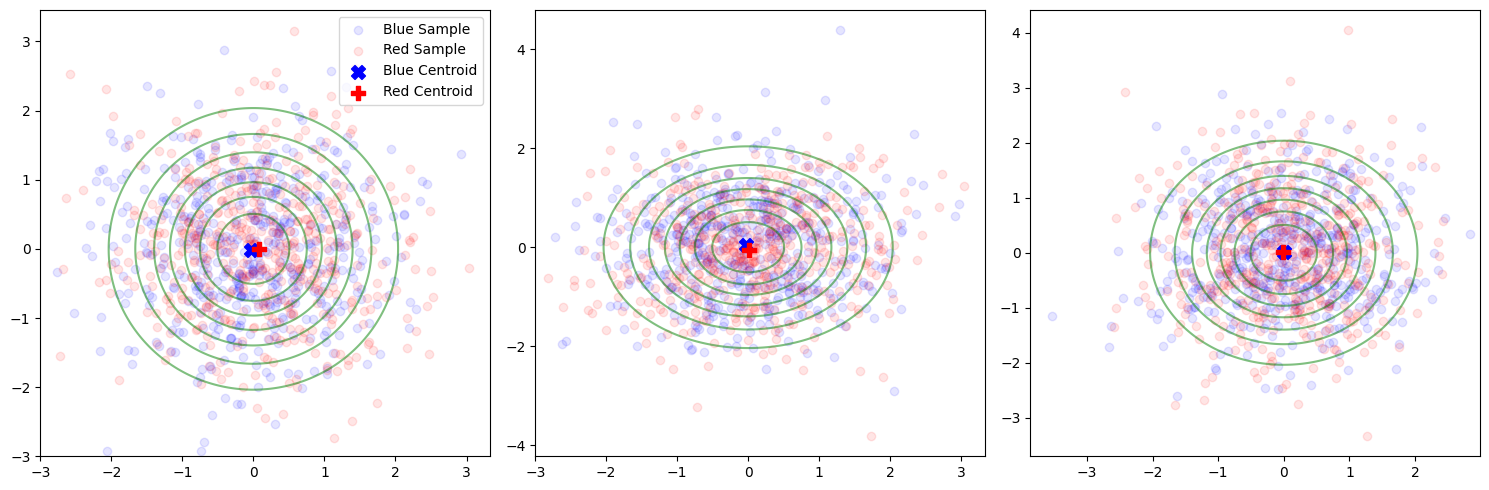
Mean Squared Error Decomposition

\(\text{MSE} = \mathbb{E}[(Y - \hat{Y})^2]\)

This can be further decomposed as:

\[ \text{MSE} = \text{Bias}^2 + \text{Variance} + \text{Irreducible Error} \]

Where:

• \(\text{Bias}(\hat{Y}) = \mathbb{E}[\hat{Y}] - Y\)
• \(\text{Variance} = \mathbb{E}[(\hat{Y} - \mathbb{E}[\hat{Y}])^2]\)

Bias-Variance Decomposition

Under and Overfitting

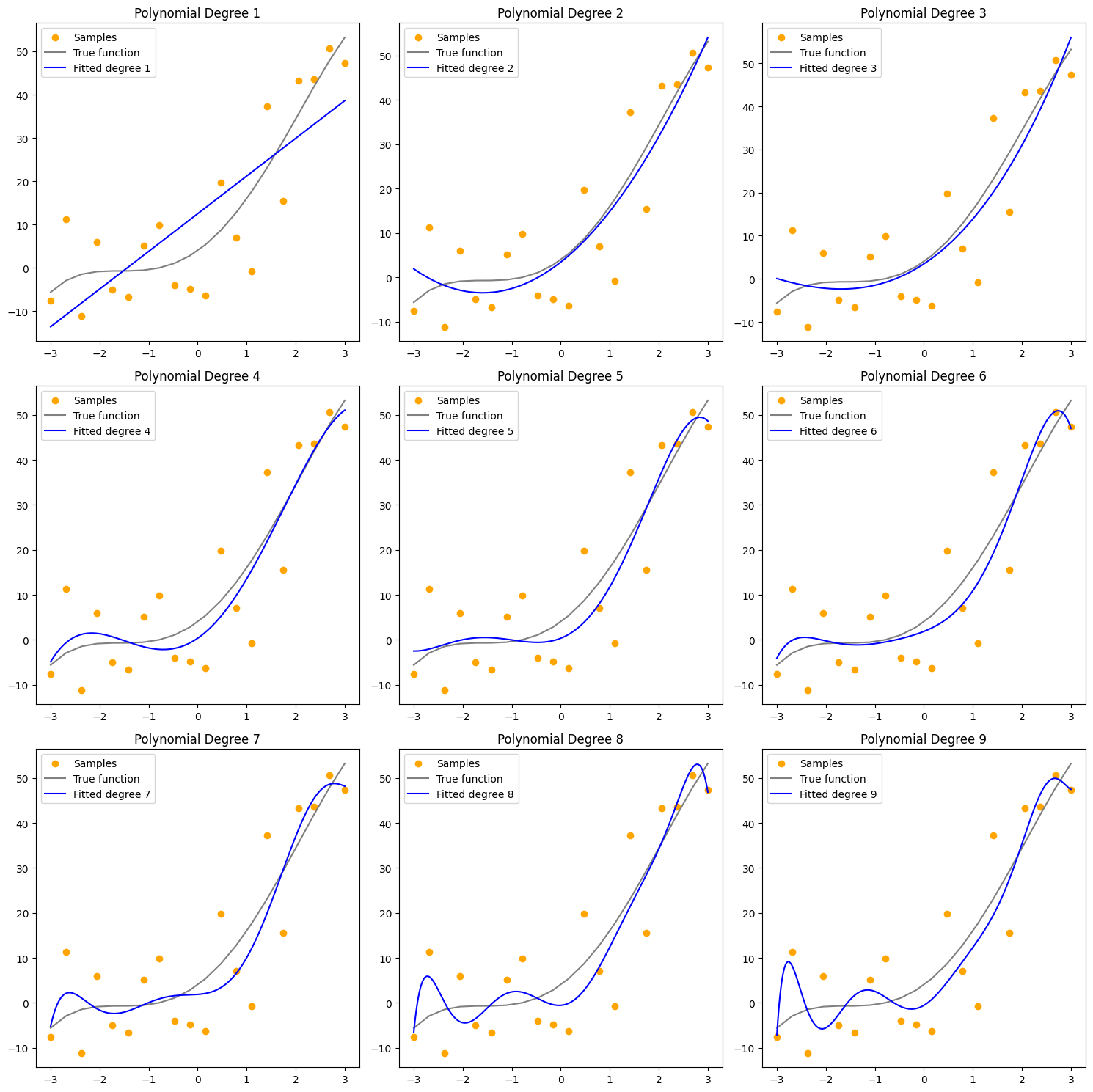
• degree 1: underfit
  • ? data true pattern
  • Higher Bias
• degree 8-9: overfit
  • random error pattern
  • Higher Variance

Under, Over and “Okay” -fitting

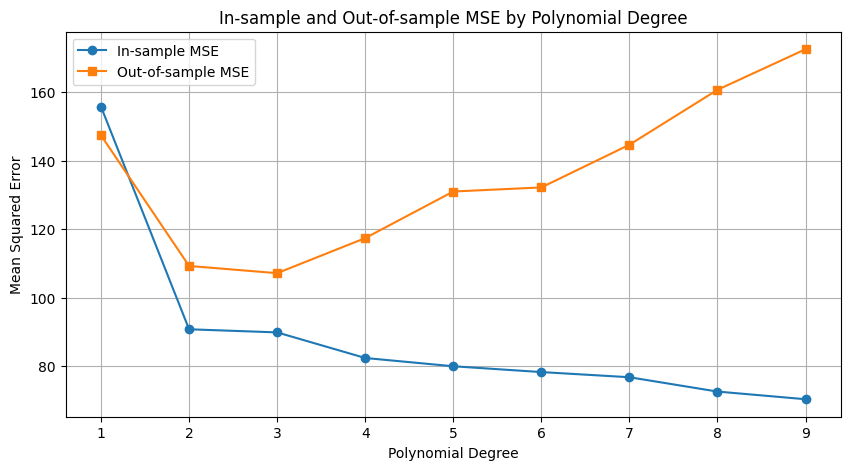
If decomposed we would see

• increased variance (out) on high degree
• increased bias (out) on low degree
• We need a “bias-variance tradeoff”

The Okay-fit is where the model:

• Learns data pattern
• Can generalize on unseen data
• Does not learn the random error pattern

WARNING: Bias variance decomposition does not always make sense.

Mandatory ML workflow

• Training data → in-sample error

• Test data → out-sample error

• Test data should be without bias

• No bias = the same error model

• Not required but recommended: adversarial datasets

Importance of bias in datasets

What is the pattern of wrong prediction ?

Importance of Explainable AI

Testing is good but explaining is better:

Importance of adversarial datasets

IMPORTANT: Adversarial datasets should come after testing.

Proper testing is done with the same underlying error.

• Why ? We are looking at different bias:
  • related to over-learning on the random error
  • not related with an error but with new data patterns
• Adversarial datasets are datasets where we can expect a new pattern in data
• Examples:
  • Wolf Images from Zoo
  • People from other countries
  • Process in another factory

ML workflow with model selection

VALIDATION IS NOT TESTING

• Model selection
• Hyperparameter tuning
• Training parameters
• Introduction of validation data
• Training split
• Re-training the selected model

Data-Driven vs Theory Driven

• Data-driven
  • Require lots of data
  • Leverage lots of algorithms
  • Require lots of computing power
  • Importance of Testing and Validation Framework
  • Hardly explainable
  • Optimizing
  • Deep Learning / Scikit-learn Pipelines
  • Business intelligence / NLP / Image

• Theory-driven
  • Can work with few data
  • Understanding of a problem
  • Require less computing power
  • Limited importance of Testing and Validation
  • Easily explainable
  • Modelling
  • Field-specific methods and algorithms
  • Aerodynamics / Molecule modeling / Genomics

B: Learning and Evaluation

ML tasks for prediction

• Classification
• Regression
• Clustering
• Association

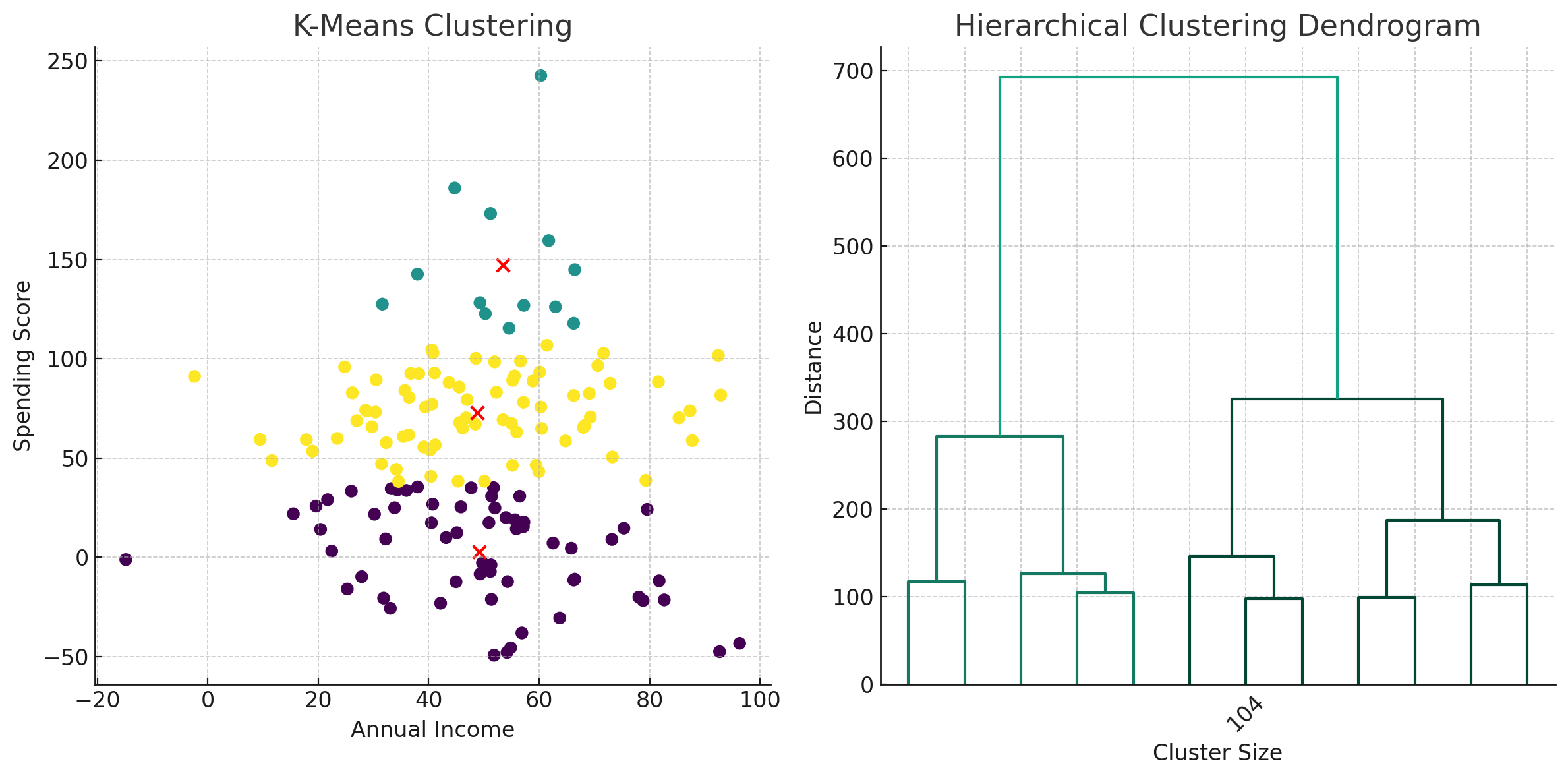
Clustering examples

• means: find groups that minimize the within-cluster sum of squares (distance to the centroid)
• Clustering
  • Compute and distance matrix (Euclidean)
  • Apply an agglomerative clustering (neighbor joining)

ML tasks for data transformation

• Data Encoding: e.g (one hot, Ordinal)

• Data Embedding:

  • Vector-representation of complex object
  • ex: Word2Vec / Encoder deep learning architecture

• Data projection: Project onto another space

  • Often based on dimensionality reduction techniques

Learning strategy

• Supervised learning
• Unsupervised
• Reinforcement learning
• Genetic Algorithm
• Transfer learning

Evaluation / Binary Classification

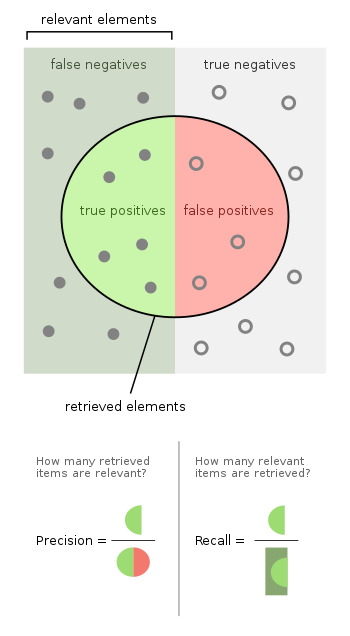
source: wikipédia

Summary metrics for Binary outcome

• Balanced single score : example F1 \[ F1 = 2 \times \frac{\text{precision} \times \text{recall}}{\text{precision} + \text{recall}} \]

• AUC: Area under curve

• ROC: Recall = f(FPR) = f(1-specificity)

• PRC: Precision = f(Recall)

Classification metrics

• Confusion Matrix
• Rand Index

Regression metrics

• Correlation (pearson / spearman)
• Distance metrics

Clustering Metrics

• Silhouette Score
• Davies-Bouldin Index

Association Metrics

• Support measures the frequency of the rule in the dataset. \[ \text{Support}(A \Rightarrow B) = \mathbb{P}(A \cap B) \]

• Confidence measures how often items in \(B\) appear in transactions that contain \(A\).

\[ \text{Confidence}(A \Rightarrow B) = \mathbb{P}(B | A) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(A)} \]

• Lift: how much more often \(A\) and \(B\) occur together than expected if they were statistically independent.

\[ \text{Lift}(A \Rightarrow B) = \frac{\mathbb{P}(B | A)}{\mathbb{P}(B)} = \frac{\mathbb{P}(B \cap A)}{\mathbb{P}(A) \mathbb{P}(B)} \]

Projection / Mapping metrics

• Continuity: Local neighborhoods preserved ?

• Mean K-Nearest Neighbors (KNN) Error: distance to centrois before and after the projection ?

Global Structure Preservation

• Correlation/Error over distance matrix

• Percentage of Variance Explained

C: ML techniques

Feature Engineering

• Feature Normalization
• Feature Selection/Extraction
• Feature Transformation
• Feature Categorization
• Feature Embedding/Encoding

Dimentionality Reduction

Curse of dimensionality: more features = more parameters

• PCA: Principal component analysis
• Principal components (PCs) are linear expressions of features
• PCs fitted so that sample variance is maximal on the first components

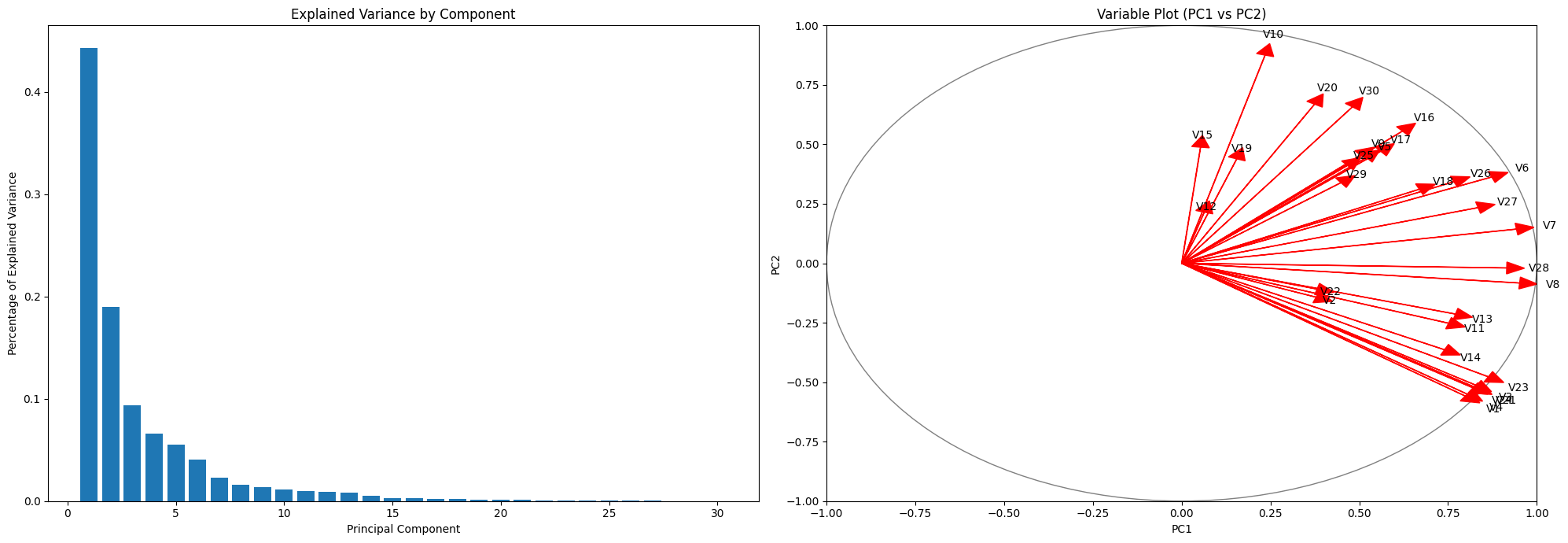
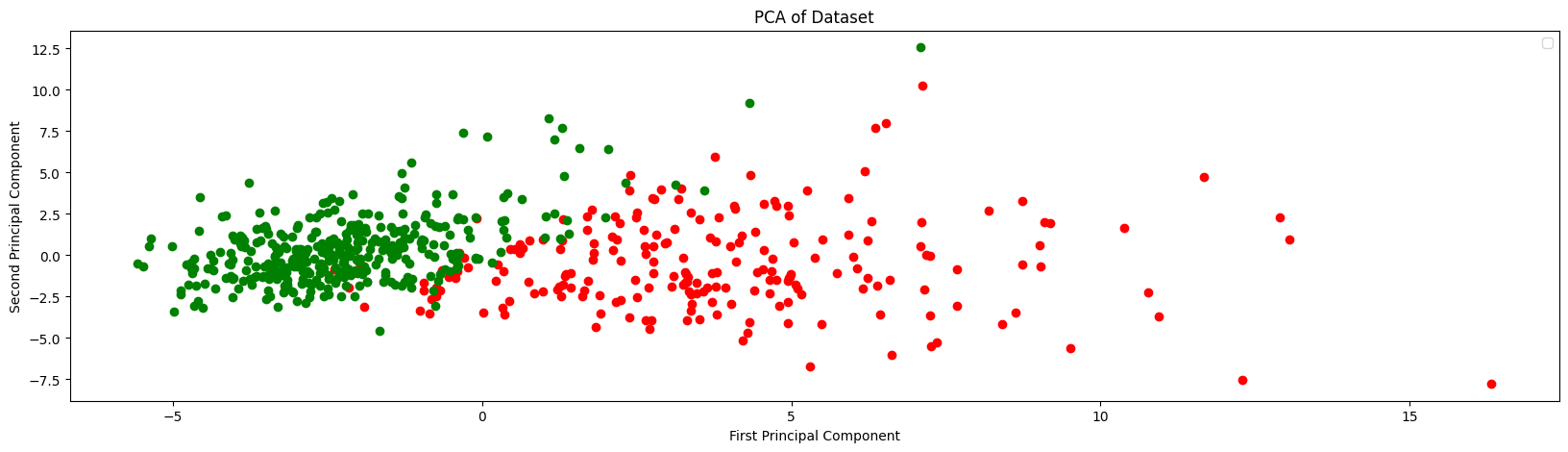
Dimensionality reduction

2 is nearly enough…

• Here samples are
• Target not used in PCA

Working with Non-Regular Data

• Imbalanced Data
  • Population bias or sample bias ?
  • Downsample ?
  • Weighting for training and
  • Use adapted algorithm (Tree-based)
• Data with Uncertainties
  • Leverage statitical models (Bayesian)
  • Sampling
  • Averaging
• Missing Data
  • Remove samples
  • Use algorithm tolerating missing data
  • Predict missing data

Model Engineering Training Setup

• Loss function and Weights
• Solver / Optimizer
• Weighting
• Other Options (e.g. tree/splits)

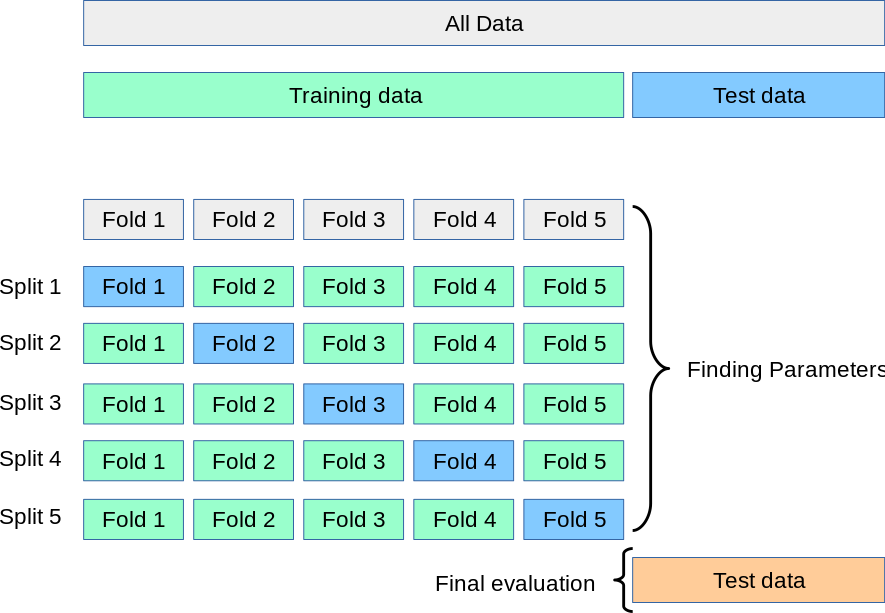
Validation and test

• Training, Validation and Test Dataset
• Cross-validation (K-Fold, Stratification) [scikit-learn]
• Challenging or Adversarial Test Dataset

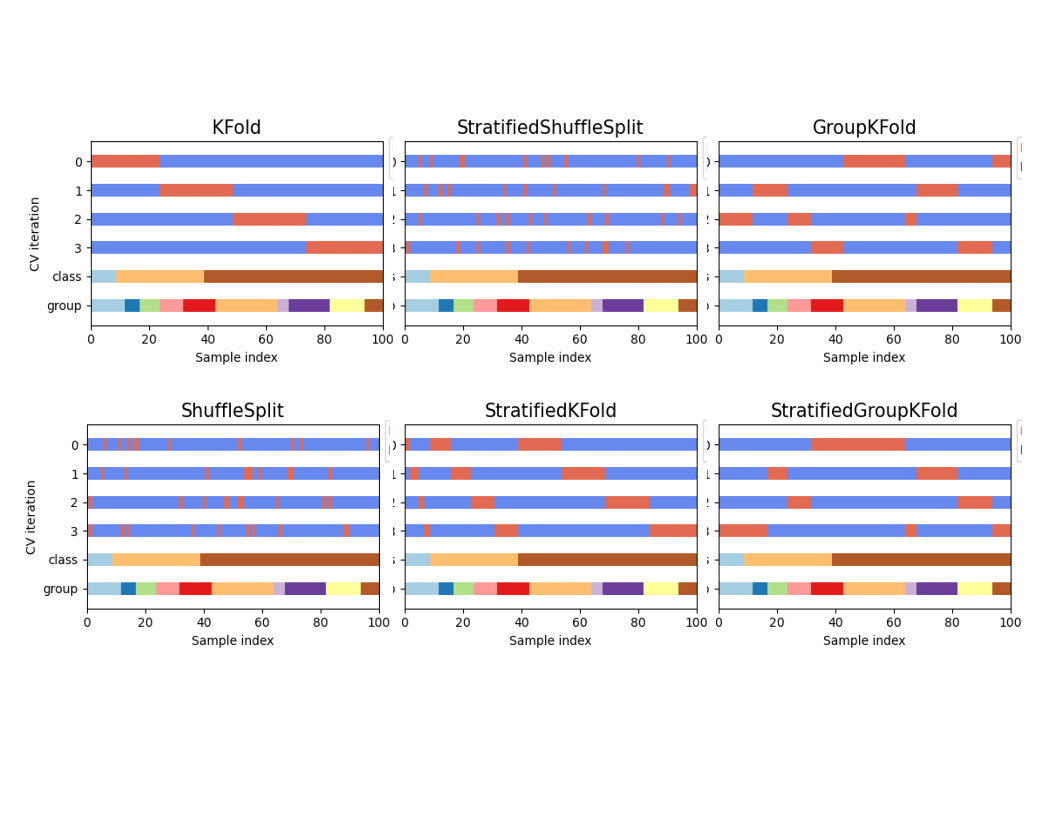
k-Fold cross-validation

Class and group in cross-validation

• Class: target
• Group: feature

Regularization

• Loss penalty

  • L1, L2 and Elastic-Net
  • Max Norm Regularization

• (Multivariate) Boundaries for optimization

• Early Stopping (for complex models)

• Drop Out (In Deep Learning)

Ensemble Learning Methods

• Principle: Aggregate Predictions
• Bagging : Bootstrap aggregating; averages predictions to reduce overfitting. (Random Forest)
• Boosting : Sequentially focuses on misclassified instances to improve accuracy. (Gradient Boosting)
• Voting : Multiple models vote on output; majority or average wins. (Decision Forest)
• Stacking : Learns from model predictions to make a final prediction. (PCA and then regression)

Stochastic Methods

• Changing the seed in a Random algorithm (SGD)
• Changing the seed for random initialization
• Boostraping
• Others: Monte Carlo simulation (Bayesian sampling)